当記事のリンクには広告が含まれています
製造業にお勤めの方は、”正規分布” とか ”ばらつき(σ)” とかは聞きなじみのあるワードかもしれません。実際、品質管理をする上でとても重要な領域であり、基礎的な統計学を知っておくのは、大量生産をしている製造メーカーさんでは重宝されるでしょう。
正直、私もこの仕事をするまでは何も知らなかったのですが、品質保証をする上で頭の片隅に入れておくべき内容かと思っております。
今日は、製造業でよく用いられる正規分布を含め基礎的な統計について解説をしていきます!
こんな方にオススメの記事
- 製造メーカーで勤務されている品質管理や生産技術、製造の方
- 現場(生産工場)にて業務を行っている方
- 工程能力指数(Cp, Cpk)を知りたい方(基礎統計を知っておく方が〇!)
- 検査工程でお仕事をされている方
はじめに
”正規分布” や “ばらつき” の具体的な話をする前に、イメージが沸きやすいように身近な例をあげて説明をしてみます。正規分布(ガウス分布とも呼ばれる)とは、確率分布の1種になります。確率分布とは、何かが起きる確率の分布のことです。
よくわかりませんよね?安心してください。簡単に説明をします!
皆さん、学生時代に嫌なテストがありましたよね?(私は嫌でした)
例えば、ここに『テストA』と『テストB』という2種類のテストがあるとします。『テストA』も『テストB』 も共に平均点数は『50点』だとします。
さて、太郎君、次郎君、花子ちゃんの 3名が『テストA』と『テストB』を受験しました。
それぞれの結果は以下となります。
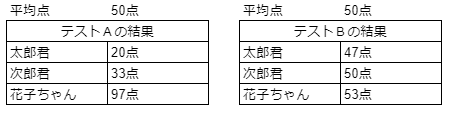
どうでしょうか? 同じ『平均点:50点』のテストでも見え方が異なりませんか。
・ テストAはめちゃくちゃ難しいテストだったけど、花子ちゃんの山が当たったのかな?
・ 太郎君も次郎君も90点代取れる優秀な生徒だったのに、体調が悪かったのかな?
・ テストBはみんな点数が取りにくい問題が多かったのかな? 等々
テストAよりテストBの方が受験した生徒の点数の “ばらつき” が少ないですね。品質観点で見ると、テストBの方が『品質が良いテスト』とみなすことができます。
この “ばらつき” は (平均値との差分)と覚えておいてください。
(正確にいうと、二乗をしたり√(ルート) を使うのですが、ここの説明では割愛します)
では、サンプル数(ここでいう生徒の数)を多くするとどうなるでしょうか?
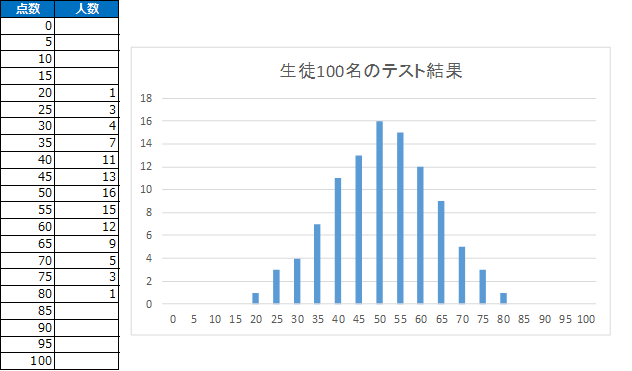
基本的には、中心が盛り上がるように山形になります。点数が極端に低い人と高い人の人数は少なく、中央に人が集まるのはイメージが付きやすいかと思います。
(ちなみに、この100人分の点数の平均は50.7点です)
この、”中心が盛り上がるように山形” や “ばらつき” が製造業の世界では非常に重要です。
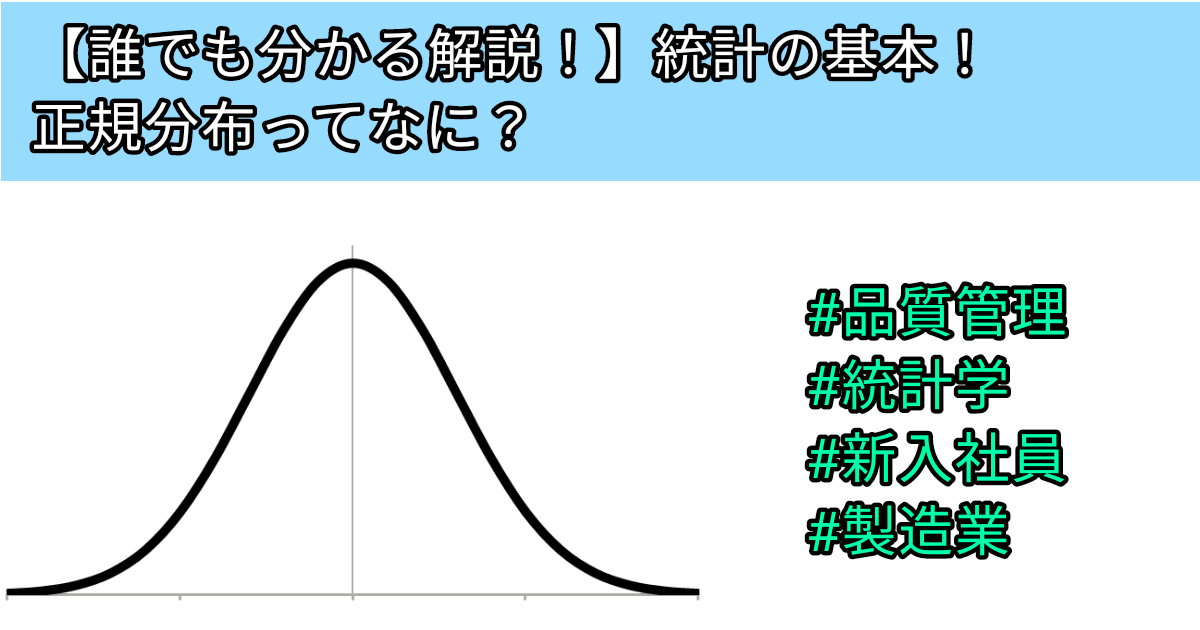
この山形に曲線を合わせてみると、滑らかな曲線になりました。
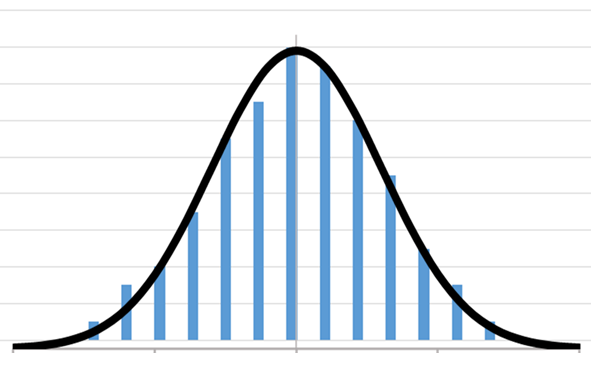
この曲線を忘れないでください。
正規分布とは?
正規分布とは、データが平均値付近に集まるように左右対称な分布の事を示す分布です。

正規分布が使われる理由は、とある決まりがあるからです。
たくさん数のある集団(母集団)から、無造作に抽出したサンプル(標本)がある程度の数を確保できると、その集団の平均値(母平均)とサンプルの平均値(標本平均)は同じ値に近づきます。
そして、この標本がある程度の数を確保できれば、正規分布に従うのです。
たくさんの生徒を集めて同じテストを受験させたとしてテスト結果を集計すると、生徒が多いほど綺麗な正規分布に近づく分布をとるのです。
ばらつき(σ)とは?
正規分布をいくつかに区切っていきます。
(1σ ~ +1σ)の範囲に、全体の 約68% が含まれます。
(-2σ ~ +2σ)の範囲に、全体の 約95% が含まれます。
(-3σ ~ +3σ)の範囲に、全体の 約99.7% が含まれます。
図で書くとこのような感じです。
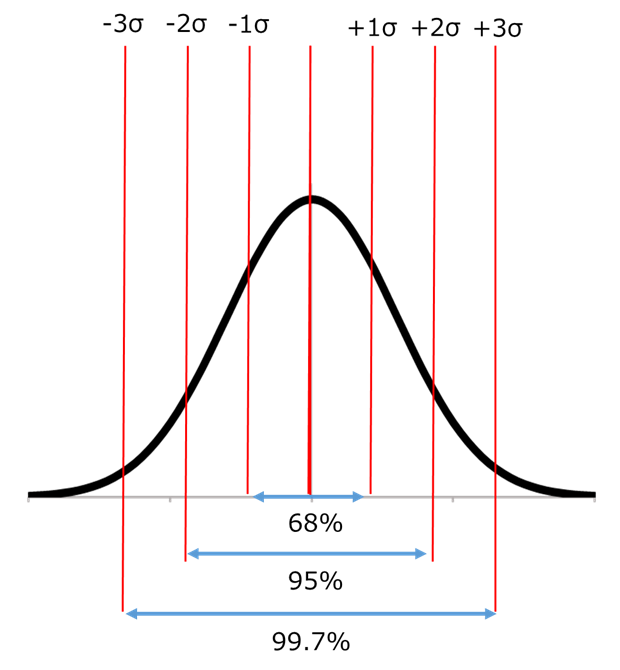
| σの範囲 | 範囲の中に入る確率 | 範囲から外れる確率 |
| ±σ | 68.3% | 31.7% |
| ±2σ | 95.4% | 4.55% |
| ±3σ | 99.73% | 0.269% |
| ±4σ | 99.993% | 0.0063% |
| ±5σ | 99.99994% | 0.000057% |
製造業にお勤めの方は、”±3σ” は聞いたことがありますね?
±3σを下限値・上限値として、その範囲内に収まるように工程で管理をすれば、不具合はほぼ起こらないとみなせるのです。
ここで説明をした “正規分布” や “ばらつき” は、工程の能力を測定したり、工程を管理するうえで非常に重要な知識となるので、頭の片隅に入れておきましょう!
まとめ
- ばらつきとは平均値との差分
- 正規分布は左右対称の山型の曲線のことをいう
- サンプル数が多かったら、その測定結果は正規分布に近づく
- 正規分布を用いることでばらつきを計算しやすくなる
- ±3σで管理をすれば、不良はほぼでない!











コメント